martes, 17 de noviembre de 2015
Las matemáticas de los siglos XIX y XX
Las matemáticas en los siglos XVIII
Durante el resto del siglo XVII y buena parte del XVIII, los discípulos de Newton y Leibniz se basaron en sus trabajos para resolver diversos problemas de física, astronomía e ingeniería, lo que les permitió, al mismo tiempo, crear campos nuevos dentro de las matemáticas. Así, los hermanos Jean y Jacques Bernoulli inventaron el cálculo de variaciones y el matemático francés Gaspard Monge la geometría descriptiva.
Joseph Louis Lagrange, también francés, dio un tratamiento completamente analítico de la mecánica en su gran obra Mecánica analítica (1788), en donde se pueden encontrar las famosas ecuaciones de Lagrange para sistemas dinámicos. Además, Lagrange hizo contribuciones al estudio de las ecuaciones diferenciales y la teoría de números, y desarrolló la teoría de grupos. Su contemporáneo Laplace escribió Teoría analítica de las probabilidades (1812) y el clásico Mecánica celeste (1799-1825), que le valió el sobrenombre de ‘el Newton francés’.
El gran matemático del siglo XVIII fue el suizo Leonard Euler, quien aportó ideas fundamentales sobre el cálculo y otras ramas de las matemáticas y sus aplicaciones. Euler escribió textos sobre cálculo, mecánica y álgebra que se convirtieron en modelos a seguir para otros autores interesados en estas disciplinas. Sin embargo, el éxito de Euler y de otros matemáticos para resolver problemas tanto matemáticos como físicos utilizando el cálculo sólo sirvió para acentuar la falta de un desarrollo adecuado y justificado de las ideas básicas del cálculo.
La teoría de Newton estaba basada en la cinemática y las velocidades, la de Leibniz en los infinitésimos, y el tratamiento de Lagrange era completamente algebraico y basado en el concepto de las series infinitas. Todos estos sistemas eran inadecuados en comparación con el modelo lógico de la geometría griega, y este problema no fue resuelto hasta el siglo posterior.
Como hemos visto, el conocimiento de los números naturales, 1, 2, 3 ,..., que aparece en las estructuras monolíticas, es más antiguo que cualquier texto escrito que se conserve. Las primeras civilizaciones - en Mesopotamia, Egipto, India y China - sabían aritmética.
Una forma de ver el desarrollo de los distintos sistemas de numeración de la matemática moderna, es ver los nuevos números estudiados e investigados para responder a preguntas sobre aritmética sbre números mas antiguos. En tiempos prehistóricos, las fracciones daban respuesta a la pregunta: ¿qué número, multiplicado por 3, da 1? En la India y China, y mucho más tarde en Alemania, los números negativos se desarrollaron para responder a la pregunta: ¿qué obtienes cuando se resta un número mayor a otro menor?
Otra pregunta natural es: ¿qué tipo de número es la raíz cuadrada de dos? Los griegos sabían que no era una fracción, y esta cuestión puede haber desempeñado un papel en el desarrollo de la fracción continua. Sin embargo, una mejor respuesta vino con la invención de los decimales, desarrollados por John Neper (1550-1617) y perfeccionados más tarde por Simon Stevin. Usando decimales, y una idea que anticipa el concepto de límite, Neper estudió una nueva constante, queLeonard Euler (1707-1783) llamó 
Euler fue muy influyente en la normalización de otros términos matemáticos y notaciones. El nombró a la raíz cuadrada de menos 1 con el símbolo  (unidad imaginaria). También popularizó el uso de la letra griega π al enunciar la razón entre la circunferencia de un círculo y su diámetro. Posteriormente, obtuvo una de las más notables identidades de las matemáticas, la identidad de Euler.
(unidad imaginaria). También popularizó el uso de la letra griega π al enunciar la razón entre la circunferencia de un círculo y su diámetro. Posteriormente, obtuvo una de las más notables identidades de las matemáticas, la identidad de Euler.
Hacia finales del siglo XVIII, Lagrange iniciaría una rigurosa teoría de funciones y de la mecánica. Ese periodo vio la gran obra de Laplace sobre mecánica celeste así como grandes progresos de Monge yCarnot en la geometría sintética.
Las matemáticas de los siglos XVII
Los europeos dominaron el desarrollo de las matemáticas después del renacimiento.
Durante el siglo XVII tuvieron lugar los más importantes avances en las matemáticas desde la era de Arquímedes y Apolonio. El siglo comenzó con el descubrimiento de los logaritmos por el matemático escocés John Napier (Neper); su gran utilidad llevó al astrónomo francés Pierre Simon Laplace a decir, dos siglos más tarde, que Neper, al reducir el trabajo de los astrónomos a la mitad, les había duplicado la vida.
La ciencia de la teoría de números, que había permanecido aletargada desde la época medieval, es un buen ejemplo de los avances conseguidos en el siglo XVII basándose en los estudios de la antigüedad clásica. La obra Las aritméticas de Diofante ayudó a Fermat a realizar importantes descubrimientos en la teoría de números. Su conjetura más destacada en este campo fue que no existen soluciones de la ecuación an+bn=cn con a, b y c enteros positivos si n es mayor que 2. Esta conjetura, conocida como último teorema de Fermat, ha generado gran cantidad de trabajos en el álgebra y la teoría de números.
En geometría pura, dos importantes acontecimientos ocurrieron en este siglo. El primero fue la publicación, en el Discurso del método(1637) de Descartes, de su descubrimiento de la geometría analítica, que mostraba cómo utilizar el álgebra (desarrollada desde el renacimiento) para investigar la geometría de las curvas (Fermat había hecho el mismo descubrimiento pero no lo publicó).
El Discurso del método, junto con una serie de pequeños tratados con los que fue publicado, ayudó y fundamentó los trabajos matemáticos de Isaac Newton hacia 1660. El segundo acontecimiento que afectó a la geometría fue la publicación, por el ingeniero francés Gérard Desargues, de su descubrimiento de la geometría proyectiva en 1639.
Otro avance importante en las matemáticas del siglo XVII fue la aparición de la teoría de la probabilidad a partir de la correspondencia entre Pascal y Fermat sobre un problema presente en los juegos de azar, el llamado problema de puntos. Este trabajo no fue publicado, pero llevó al científico holandés Christiaan Huygens a escribir un pequeño folleto sobre probabilidad en juegos con dados, que fue publicado en el Ars coniectandi (1713) del matemático suizo Jacques Bernoulli.
Tanto Bernoulli como el francés Abraham De Moivre, en su Doctrina del azar de 1718, utilizaron el recién descubierto cálculo para avanzar rápidamente en su teoría, que para entonces tenía grandes aplicaciones en pujantes compañías de seguros.
Sin embargo, el acontecimiento matemático más importante del siglo XVII fue, sin lugar a dudas, el descubrimiento por parte de Newton de los cálculos diferencial e integral, entre 1664 y 1666. Newton se basó en los trabajos anteriores de dos compatriotas, John Wallis e Isaac Barrow, así como en los estudios de otros matemáticos europeos como Descartes, Francesco Bonaventura Cavalieri, Johann van Waveren Hudde y Gilles Personne de Roberval.
Unos ocho años más tarde, el alemán Gottfried Wilhelm Leibniz descubrió también el cálculo y fue el primero en publicarlo, en 1684 y 1686. El sistema de notación de Leibniz es el que se usa hoy en el cálculo.
Las matemáticas en el renacimiento
 Aunque el final del periodo medieval fue testigo de importantes estudios matemáticos sobre problemas del infinito por autores como Nicole Oresme, no fue hasta principios del siglo XVI cuando se hizo un descubrimiento matemático de trascendencia en Occidente. Era una fórmula algebraica para la resolución de las ecuaciones de tercer y cuarto grado, y fue publicado en 1545 por el matemático italiano Gerolamo Cardano en su Ars magna.
Aunque el final del periodo medieval fue testigo de importantes estudios matemáticos sobre problemas del infinito por autores como Nicole Oresme, no fue hasta principios del siglo XVI cuando se hizo un descubrimiento matemático de trascendencia en Occidente. Era una fórmula algebraica para la resolución de las ecuaciones de tercer y cuarto grado, y fue publicado en 1545 por el matemático italiano Gerolamo Cardano en su Ars magna.
Este hallazgo llevó a los matemáticos a interesarse por los números complejos y estimuló la búsqueda de soluciones similares para ecuaciones de quinto grado y superior. Fue esta búsqueda la que a su vez generó los primeros trabajos sobre la teoría de grupos a finales del siglo XVIII y la teoría de ecuaciones del matemático francés Évariste Galois a principios del XIX.
También durante el siglo XVI se empezaron a utilizar los modernos signos matemáticos y algebraicos. El matemático francés François Viète llevó a cabo importantes estudios sobre la resolución de ecuaciones. Sus escritos ejercieron gran influencia en muchos matemáticos del siglo posterior, incluyendo a Pierre de Fermat en Francia e Isaac Newton en Inglaterra.
el álgebra
Las actividades matemáticas no solo lograron significativos avances en el área del álgebra, sino que también en la trigonometría y la geometría.
Ya se utiliza un simbolismo básico y simple en álgebra, los símbolos indo-arábigos están suficientemente extendidos, las fracciones decimales se desarrollan lentamente y la teoría de las ecuaciones ha logrado comprender la solución general de la cúbica y la bicuadrática.
Ya se utiliza un simbolismo básico y simple en álgebra, los símbolos indo-arábigos están suficientemente extendidos, las fracciones decimales se desarrollan lentamente y la teoría de las ecuaciones ha logrado comprender la solución general de la cúbica y la bicuadrática.
Los números negativos son aceptados progresivamente y la trigonometría, considerada ciencia independiente, dispone ya de tablas muy precisas para las seis funciones. En cuanto a la geometría, se desarrollan nuevas orientaciones en geometría descriptiva y proyectiva. Es válido destacar que sin el acceso a la imprenta, todos estos avances no podrían haber sido tan ampliamente difundidos entre las personas.
La aplicación de todos estos conocimientos a campos tan diversos como la cartografía, el arte, la óptica o la contabilidad sirvió para relanzar las matemáticas y darles un impulso de modernidad, sustituyendo los modelos clásicos por unos que contengan un sentído más crítico.
François Viète contribuyó enormemente a esta etapa de la culminación del Renacimiento y comienzo de las matemáticas modernas.
La notación algebraica, un paso importante
El álgebra hasta el siglo XVI era de tipo verbal, en realidad, el álgebra todavía no estaba muy diferenciada de la geometría. La incógnita de un problema era pensada como la longitud de un segmento de recta; el cuadrado de la incógnita se refería al área de un cuadrado y su cubo, al volúmen de un cubo. Desde este escaso punto de vista, tanto números negativos como potencias más grandes a tres eran imposibles de ser razonadas. Además, un cuadrado no podía ser sumado con un cubo es decir no se podía sumar x2+x3, debido a que áreas y volúmenes son cantidades de diferente notaciones y no pueden ser combinadas. Así, el álgebra era todavía un conjunto específico de reglas que eran usadas para resolver ecuaciones particulares. Un avance importante se dio hacia el final del siglo XVI: el álgebra vino a ser una herramienta muy poderosa pues se le proveyó de un mayor simbolismo. Se introdujo la notación exponencial y lo que se escribía como ” A cubus” o “AAA ” podría ser ahora escrito como A3, en pocas palabras, fue una gran simplificación, mejora y modernización . Los símbolos +, –, = fueron también introducidos. Este último fue propuesto por Robert Recorde, quien decía que no existen dos cosas tan iguales, identicas, que dos lineas paralelas.

la trigonometria
Con relación a la trigonometría debe decirse que, aunque los peritos usaban los métodos geométricos romanos, se empezó a usar algo de trigonometría plana con un método iniciado por Leonardo de Pisa en su Practica Geometriae (1 220).
Otros avances fueron hechos por el mismo George Peurbach (1423 - 1461) de Viena, quien ofreció tablas trigonométricas más precisas y corrigió algunas traducciones latinas delAlmagesto que habían sido realizadas desde versiones árabes y no griegas.
El más conocido, sin embargo, fue Johannes Müller (1436 - 1476), el famoso Regiomontano, que fue discípulo de Peurbach y del cardenal Bessarion (c. 1400 - 1472). Regiomontano no solo haría varias traducciones de obras griegas sino que también estableció su propia imprenta para imprimirlas. Entre ellas las Secciones Cónicas de Apolonio y partes de Arquímedes y Herón. Se sabe que en su libro De Triangulis, 1462 - 1463, Regiomontano se benefició de algunos trabajos árabes para expresar de una mejor manera el conocimiento disponible sobre trigonometría plana, geometría esférica, y trigonometría esférica.
Un detalle sobre Müller: Nicolás de Cusa (1401 - 1464), quien se supone fue el primer europeo que buscó resolver el problema clásico de la cuadratura del círculo, y un intelectual, incluso cardenal, que tendría importantes repercusiones, fue corregido por Regiomontano (1436 - 1476), quien le señaló algunos problemas o errores de razonamiento.
La construcción de tablas fue otro asunto importante durante los siglos XV y XVI. Por ejemplo, laboraron en eso George Joachim Rheticus (1514 - 1576), Copérnico, François Vieta (1540 - 1603) y Barthdolomaeus Pitiscus (1561 - 1613). En estos trabajos usaron números de unidades muchísimo más largos en el radio, de tal forma que los valores de las cantidades trigonométricas pudieran ser obtenidas con mayor precisión sin usar fracciones o decimales. Rheticus calculó una tabla de senos basado sobre un radio de diez a la diez unidades y otro basado en diez a la 15 unidades y dio valores para cada diez segundos del arco. Pitiscus corrigió algunos de estos trabajos. Se supone, precisamente, que la palabra trigonometría fue dada por él.
Un detalle interesante con Rheticus es que cambió el significado del seno. Antes se usaba como el seno del arco y no del ángulo (en una circunferencia), ahora era el seno del ángulo.
Más adelante toda la trigonometría plana y esférica fue sistematizada y extendida por Vieta. Su obra Canon Mathematicus (1 579) ofrece las fórmulas para la solución de los triángulos planos recto y oblicuo y la ley de las tangentes, elaborada por él mismo. Vieta ofreció más identidades trigonométricas que las que había establecido Ptolomeo.
Tal vez, lo más importante a señalar de la trigonometría del siglo XVI es su separación de la astronomía y su evolución como una rama propia de las matemáticas. No es que ésta ya no se usara en la astronomía, sino que era aplicada en otras dimensiones adicionales como, por ejemplo, la topografía.
la geometría en el renacimiento
El arte medieval era profundamente religioso, la representación de la realidad y del hombre no eran importantes, Dios y los santos eran figuras adoradas, pero su representación o era irreal o estaba idealizada, esbeltas figuras para ser vistas desde la perspectiva inferior en las iglesias, los artistas poco a poco fueron haciéndose mas profesionales y dedicados, las horribles pinturas mal proporcionadas eran la norma, Giotto di Bondone fue el primer pintor que redescubrió el realismo griego, sus obras volvían a presentar las figuras humanas en sus proporciones correctas, por su belleza y proporción geométrica, es considerado la primera luz de la razón en las edades obscuras, su arte fue el nacimiento de lo que con el tiempo se llamaría Renacimiento.
La matemática está en el origen de toda cultura, sin precisos conocimientos de geometría, aritmética y trigonometría, es imposible crear una hermosa catedral, una figura escultórica con una forma humana exacta o reproducir la hermosa realidad de una pintura de Ucello, Miguel Ángel o Rafael.

LAS BASES: Piero della Francesca
Los pintores renacentistas se dieron cuenta de que la realidad de la naturaleza es geométrica, el horizonte es una línea recta, el sol y la luna esferas, los edificios son rectas y planos, los cuerpos de los animales son círculos matizados e incluso el cuerpo humano son esferas, cilindros y demás, Piero della Francesca encontró que todo ello obedecía a determinadas leyes matemáticas, como el punto de fuga; escribió libros de arte que son obras de matemática precisa.


LA PERFECCION DE LA MATEMATICA: UCELLO
Si alguien estudio con detalle la formas simples de la naturaleza, este fue Paolo Ucello, sus obras son elaboradas aplicaciones de la perfección geométrica, en el estudio para la estatua de Hawkwood, el caballo está pintado siguiendo círculos y elipses, el gorro es un masaccio, las bases son cuadrángulos, las fuentes parábolas y elipses, sus obras son hermosas realizaciones del más puro arte geométrico.

Ucello planeaba cuidadosamente sus obras, creando esquemas previos en los que hacia estudios detallados de las secciones rectas, formas y figuras, mucho antes de siquiera tocar el pincel, comprendio profundamente el significado de la geometria en la representacion de la realidad.

En sus obras hay cierto sabor a geometria pura, como puede sentirse en el Diluvio, notese el punto de fuga ligeramente arriba del centro del cuadro, y el Massacio alrededor del cuello de la figura en primer plano.

EL PUNTO DE FUGA
La realidad establece leyes estrictas, como lo son las matemáticas; el punto de fuga fue uno de los primeros descubrimientos, los objetos entre más lejanos, son más pequeños, pero obedeciendo los conceptos geométricos de las rectas, el tamaño real disminuye linealmente, al colocar un punto de convergencia en la pintura, hacia el que tienden todas las rectas del cuadro, se crea una perfeccion matematica.


LEONARDO EL TOQUE DEL GENIO
Si los primeros pintores del Renacimiento eran inteligentes, los pintores del alto renacimiento como Leonardo, Rafael, Caravaggio, Miguel Ángel; Van Eyck o Rembrant, lograron algunos de los momentos más elevados del espíritu humano, sus obras están llenas de las más profundas emociones humanas, y de geometría, la Virgen de la Rocas de Leonardo es un magnifico resumen del Renacimiento, juega con la simetría, los puntos de fuga múltiples, la geometría básica se ha llevado hasta un punto en que la ternura de la virgen es una unión entre el color, la esfera, la luz y los sentimientos.
las matemáticas en la edad media
2.1 las matemáticas en india y china
La India y las matemáticas
Son muy escasos los documentos de tipo matemático que han llegado a nuestras manos, pese a tener constancia del alto nivel cultural de esta civilización. Aun más que en el caso de China, existe una tremenda falta de continuidad en la tradición matemática hindú y al igual que ocurría con las tres civilizaciones anteriores, no existe ningún tipo de formalismo teórico.
Los primeros indicios matemáticos se calculan hacia los siglos VIII-VII a.C, centrándose en aplicaciones geométricas para la construcción de edificios religiosos y también parece evidente que desde tiempos remotos utilizaron un sistema de numeración posicional y decimal.
Fue, sin embargo, entre los siglos V-XII d.C cuando la contribución a la evolución de las matemáticas se hizo especialmente interesante, destacando cuatro nombres propios: Aryabhata (s.VI), Brahmagupta (s.VI), Mahavira (s. IX) y Bhaskara Akaria (s.XII).
La característica principal del desarrollo matemático en esta cultura, es el predominio de las reglas aritméticas de cálculo, destacando la correcta utilización de los números negativos y la introducción del cero, llegando incluso a aceptar como números validos las números irracionales.
Profundizaron en la obtención de reglas de resolución de ecuaciones lineales y cuadráticas, en las cuales las raíces negativas eran interpretadas como deudas. Desarrollaron también, sin duda para resolver problemas astronómicos, métodos de resolución de ecuaciones diofánticas, llegando incluso a plantear y resolver (s.XII) la ecuación x2=1+ay2, denominada ecuación de Pelt.
Como resumen acabaremos diciendo que en la historia de la India se encuentran suficientes hechos que ponen en evidencia la existencia de relaciones políticas y económicas con los estados griegos, egipcios, árabes y con China. Matemáticamente se considera indiscutible la
procedencia hindú del sistema de numeración decimal y las reglas de cálculo.
China y las matemáticas
Aunque la civilización china es cronológicamente comparable a las civilizaciones egipcia y mesopotámica, los registros existentes son bastante menos fiables.
La primera obra matemática es "probablemente" el Chou Pei (horas solares) ¿1200 a.C.? y junto a ella la más importante es "La matemática de los nueve libros" o de los nueve capítulos. Esta obra, de carácter totalmente heterogéneo, tiene la forma de pergaminos independientes y están dedicados a diferentes temas de carácter eminentemente práctico formulados en 246 problemas concretos, a semejanza de los egipcios y babilónicos y a diferencia de los griegos cuyos tratados eran expositivos, sistemáticos y ordenados de manera lógica.
Los problemas resumen un compendio de cuestiones sobre agricultura, ingeniería, impuestos, cálculo, resolución de ecuaciones y propiedades de triángulos rectángulos.
 El sistema de numeración es el decimal jeroglífico. Las reglas de las operaciones son las habituales, aunque destaca como singularidad, que en la división de fracciones se exige la previa reducción de éstas a común denominador.
El sistema de numeración es el decimal jeroglífico. Las reglas de las operaciones son las habituales, aunque destaca como singularidad, que en la división de fracciones se exige la previa reducción de éstas a común denominador.
Dieron por sentada la existencia de números negativos, aunque nunca los aceptaron como solución a una ecuación
La contribución algebraica más importante es, sin duda, el perfeccionamiento alcanzado en la regla de resolución de sistemas de ecuaciones lineales. Para todos los sistemas se establece un método genérico de resolución muy similar al que hoy conocemos como método de Gauss, expresando incluso los coeficientes en forma matricial, transformándolos en ceros de manera escalonada.
Inventaron el "tablero de cálculo", artilugio consistente en una colección de palillos de bambú de dos colores (un color para expresar los números positivos y otro para los negativos) y que podría ser considerado como una especie de ábaco primitivo.
Esta orientación algorítmica de las matemáticas en la China Antigua, se mantiene hasta mediados del siglo XIV debido fundamentalmente a las condiciones socio-económicas de esta sociedad.
Con el desarrollo del "método del elemento celeste" se culminó el desarrollo del álgebra en China en la edad media. Este método, desarrollado por Chou Shi Hié, permitía encontrar raíces no sólo enteras, sino también racionales, e incluso aproximaciones decimales para ecuaciones de la forma Pn(x)=a4x4+a3x3+a2x2+a1x+ao .
El método del elemento celeste es equivalente al que en Occidente denominamos "método de Horner", matemático que vivió medio siglo más tarde.
Otro gran logro de la época medieval fue la suma de progresiones desarrollado por Chon Huo (s. XI) y Yang Hui (s.XIII). Unido a estas sumas de progresiones se establecieron elementos sólidos en la rama de la combinatoria, construyendo el llamado "espejo precioso" de manera similar al que hoy conocemos como triángulo de Tartaglia o Pascal.
No se puede decir que la geometría fuese el punto fuerte de la cultura china, limitándose principalmente a la resolución de problemas sobre distancias y semejanzas de cuerpos.
Aproximadamente a mediados del siglo XIV comenzó en China un largo periodo de estancamiento.
2.2 Matemática en el islam medieval

La matemática en el Islam medieval también conocida como matemática árabe o matemática musulmán se enriqueció en forma creciente a medida que los musulmanes conquistaron territorios. Con rapidez inusitada, el imperio islámico se expandió en todo el territorio que se extiende por las orillas del Mediterráneo, desde Persia hasta los Pirineos.
desarrollos y contexto histórico
En 642 los árabes ocuparon Alejandría, con lo que recogieron la huella de la cultura griega, para después prolongarla y perfeccionarla.

 Los antecedentes de los desarrollos matemáticos que comenzaron en Bagdad alrededor del año 800 no son aún demasiado claros. Ciertamente que hubo una poderosa influencia proveniente de los matemáticos de la India, cuyo temprano desarrollo de la notación posicional y uso del cero, revistieron gran importancia. Allí comenzó un período de progreso matemático con el trabajo de al-Jwarizmi y la traducción de los textos griegos.
Los antecedentes de los desarrollos matemáticos que comenzaron en Bagdad alrededor del año 800 no son aún demasiado claros. Ciertamente que hubo una poderosa influencia proveniente de los matemáticos de la India, cuyo temprano desarrollo de la notación posicional y uso del cero, revistieron gran importancia. Allí comenzó un período de progreso matemático con el trabajo de al-Jwarizmi y la traducción de los textos griegos.
En 762 Al-Mansur, el décimo califa se instaló en Bagdad. Recogiendo los restos de la ciencia alejandrina, convirtió a Bagdad en una capital científica. Harún al-Rashid, quinto califa de la dinastía Abásida, comenzó su reinado el 14 de septiembre de 786. Promovió la investigación científica y la erudición. Las primeras traducciones de textos griegos al árabe, como los Elementos de Euclides por al-Hajjaj, fueron hechas durante su reinado. El séptimo califa, Abd Allah al-Ma'mun, alentó la búsqueda del conocimiento científico aún más que su padre al-Rashid, estableciendo en Bagdad una institución de investigación y traducción: la Casa de la Sabiduría (Bayt al-Hikma). Allí trabajaron al-Kindi y los tres hermanos Banu Musa, así como el famoso traductor Hunayn ibn Ishaq.
En la Casa se tradujeron las obras de Euclides, Diofanto, Menelao, Arquímedes, Ptolomeo, Apolonio, Diocles, Teodosio,Hipsicles y otros clásicos de la ciencia griega. Es necesario enfatizar que estas traducciones fueron hechas por científicos, no por expertos en lenguas ignorantes de las matemáticas, y la necesidad de estas traducciones fue estimulada por las investigaciones más avanzadas de la época.
Uno de los avances más significativos llevados a cabo por los matemáticos del islam (y, sin duda, uno de los más trascendentes en toda la historia de la ciencia) tuvo origen en esa época, con los trabajos de Abu Yafar Mohamed ibn Musa al-Jwarizmi: el álgebra. Es importante entender que la nueva idea representaba un apartamiento revolucionario del concepto geometricista de los griegos. El álgebra era una teoría unificadora que permitió que los números racionales, los irracionales, las magnitudes geométricas, etc. fuesen tratados como «objetos algebraicos». Ella abrió caminos de desarrollo matemático hasta entonces desconocidos; como señala Rashed:4
Los sucesores de al-Jwarizmi emprendieron una aplicación sistemática de la aritmética al álgebra, del álgebra a la aritmética, de ambas a la trigonometría, del álgebra a la teoría de números euclidiana, del álgebra a la geometría, y de la geometría al álgebra. Fue así como se crearon el álgebra polinomial, el análisis combinatorio, el análisis numérico, la solución numérica de ecuaciones, la nueva teoría elemental de números, y la construcción geométrica de ecuaciones.
Alrededor de 40 años después de al-Jwarizmi, aparecerán los trabajos de al-Mahani (nacido en 820), quien concibió la idea de reducir los problemas geométricos como el de la duplicación del cubo a problemas de álgebra. Abu Kamil, nacido en 850, constituye un vínculo importante en el desarrollo del álgebra entre al-Jwarizmi y al-Karaji. Pese a no usar símbolos (escribía en palabras las potencias de  ) fue quien comenzó a entender lo que en símbolos actuales escribiríamos como
) fue quien comenzó a entender lo que en símbolos actuales escribiríamos como  . Nótese que los símbolos no habrán de aparecer en las matemáticas del islam hasta mucho después. Ibn al-Banna y al-Qalasadi usaban símbolos en el siglo XV, y es sabido que fueron empleados al menos un siglo antes que estos cientíicos los usaran (en Occidente aparecerían por primera vez en 1591, es decir, no menos de dos siglos más tarde. Su «invención» se atribuye al matemático francés François Viète.
. Nótese que los símbolos no habrán de aparecer en las matemáticas del islam hasta mucho después. Ibn al-Banna y al-Qalasadi usaban símbolos en el siglo XV, y es sabido que fueron empleados al menos un siglo antes que estos cientíicos los usaran (en Occidente aparecerían por primera vez en 1591, es decir, no menos de dos siglos más tarde. Su «invención» se atribuye al matemático francés François Viète.
 ) fue quien comenzó a entender lo que en símbolos actuales escribiríamos como
) fue quien comenzó a entender lo que en símbolos actuales escribiríamos como  . Nótese que los símbolos no habrán de aparecer en las matemáticas del islam hasta mucho después. Ibn al-Banna y al-Qalasadi usaban símbolos en el siglo XV, y es sabido que fueron empleados al menos un siglo antes que estos cientíicos los usaran (en Occidente aparecerían por primera vez en 1591, es decir, no menos de dos siglos más tarde. Su «invención» se atribuye al matemático francés François Viète.
. Nótese que los símbolos no habrán de aparecer en las matemáticas del islam hasta mucho después. Ibn al-Banna y al-Qalasadi usaban símbolos en el siglo XV, y es sabido que fueron empleados al menos un siglo antes que estos cientíicos los usaran (en Occidente aparecerían por primera vez en 1591, es decir, no menos de dos siglos más tarde. Su «invención» se atribuye al matemático francés François Viète.
Abu Bekr ibn Muhammad ibn al-Husayn al-Karaji, nacido en 953, es probablemente el primero en liberar completamente al álgebra de las operaciones geométricas y remplazarlas por el tipo de operaciones aritméticas que constituyen el corazón del álgebra actual. Fue el primero en definir los monomios 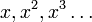 ; y
; y 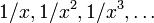 , y proporcionar reglas para el producto de dos cualesquiera de ellos. Inició una escuela algebraica que florecería por varios siglos. Cerca de doscientos años después, un importante miembro de la escuela de al-Karaji, al-Samawal (nacido en 1130) fue el primero en dar al nuevo tópico del álgebra una descripción precisa, cuando escribió que ella se ocupaba
, y proporcionar reglas para el producto de dos cualesquiera de ellos. Inició una escuela algebraica que florecería por varios siglos. Cerca de doscientos años después, un importante miembro de la escuela de al-Karaji, al-Samawal (nacido en 1130) fue el primero en dar al nuevo tópico del álgebra una descripción precisa, cuando escribió que ella se ocupaba
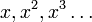 ; y
; y 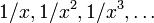 , y proporcionar reglas para el producto de dos cualesquiera de ellos. Inició una escuela algebraica que florecería por varios siglos. Cerca de doscientos años después, un importante miembro de la escuela de al-Karaji, al-Samawal (nacido en 1130) fue el primero en dar al nuevo tópico del álgebra una descripción precisa, cuando escribió que ella se ocupaba
, y proporcionar reglas para el producto de dos cualesquiera de ellos. Inició una escuela algebraica que florecería por varios siglos. Cerca de doscientos años después, un importante miembro de la escuela de al-Karaji, al-Samawal (nacido en 1130) fue el primero en dar al nuevo tópico del álgebra una descripción precisa, cuando escribió que ella se ocupaba2.3 las matemáticas en Europa
temprana edad media (500-1100)
Boethius siempre tuvo un lugar para las matemáticas en el plan de estudios cuando se acuñó el término "quadrivium" para describir el estudio de la aritmética, la geometría, la astronomía, y la música. Él escribió De institutione arithmetica, una traducción libre del griego de la Introducción a la Aritmética de Nicomachus; De institutione musica, también procedente de fuentes griegas, y una serie de extractos de la Geometría de Euclides. Sus obras fueron teóricas, más que prácticas, y fueron la base del estudio matemático hasta la recuperación de las obras matemáticas griegas y árabes.
renacimiento de las matemáticas en Europa
En el siglo XII, los estudiosos europeos viajaron a España y Sicilia en busca de textos científicos árabes, incluyendo el al-Jabr wa-al-Muqabilah del matemático Al-Khwarizmi, traducido al latín por Robert de Chester, y el texto completo de los Elementos de Euclides, traducidos en varias versiones por Adélard de Bath, Herman de Carintia, y Gerard de Cremona.
Estas nuevas fuentes provocaron una renovación de la matemática. Fibonacci, con el Liber Abaci, escrito en 1202 y actualizado en 1254, elaboró las primeras matemáticas significativas en Europa desde la época de Eratóstenes, un lapsus de más de un millar de años. Su trabajo introdujo la numeración arábico-hindú en Europa, y se debatieron muchos otros problemas matemáticos.
El siglo XIV vio el desarrollo de nuevos conceptos matemáticos para investigar una amplia gama de problemas. Un área importante que contribuyó al desarrollo de la matemática fue el del análisis del movimiento local. Thomas Bradwardine propone que la velocidad (v) aumenta en progresión aritmética mientras que la razón entre la fuerza (F) y la resistencia (R) aumentan en progresión geométrica. Bradwardine expresó esto por medio de una serie de ejemplos concretos, pero, aunque el logaritmo todavía no se había concebido, podemos expresar su conclusión anacrónicamente de la siguiente forma:
El análisis de Bradwardine es un ejemplo de como la técnica utilizada por al-Kindi y Arnald de Villanova para cuantificar la naturaleza de los medicamentos compuestos, se traslada a un problema físico diferente.
Uno de los calculadores de Oxford del siglo XIV, William Heytesbury, carente de cálculo diferencial y del concepto de límite, propuso para medir la velocidad instantánea "de la ruta que describe un cuerpo si se traslada de manera uniforme con la misma rapidez con que se mueve en ese instante dado"
Heytesbury y otros determinaron matemáticamente la distancia recorrida por un cuerpo en movimiento uniformemente acelerado (lo que nosotros hoy resolveríamos mediante una simple integral), afirmando que "un cuerpo en movimiento que adquiere o pierde de manera uniforme ese incremento de velocidad recorrerá en un momento dado una distancia completamente igual a la que recorrería si se desplazase de forma continua durante el mismo tiempo con la media de la velocidad".
Nicole Oresme de la Universidad de París y el italiano Giovanni di Casali proporcionaron de manera independientemente demostraciones de esta relación, afirmando que el área bajo la línea que representa la aceleración constante, representaba la distancia total recorrida. En un comentario posterior sobre las matemáticas de la Geometría de Euclides , Oresme hizo un más detallado análisis general en el que demostró que un cuerpo adquirirá en cada sucesivo incremento de tiempo un incremento de cualquier cualidad que aumenta como los números impares. Como Euclides había demostrado que la suma de los números impares son los números cuadrados, el total de la calidad adquirida por el cuerpo aumenta como el cuadrado del tiempo
Suscribirse a:
Entradas (Atom)
